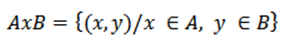UNIDAD 4 RELACIONES Y FUNCIONES

Temática

4.1 Par Ordenado

¿Qué es un par ordenado?

Un par ordenado es un arreglo ordenado de elementos de la forma (a, b) en donde “a”,  corresponde a la primera componente y se la llama abscisa, y b es la segunda componente y es llamada ordenada.

Plano Cartesiano:

El plano cartesiano está formado por dos rectas perpendiculares, una horizontal y otra vertical que se cortan en un punto, llamado origen. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.

4.2 Producto Cartesiano.

El producto cartesiano de dos conjuntos A y B (se simboliza AxB) es el conjunto de todas las parejas ordenadas (x, y), tales que x pertenece al primer conjunto A y “y” pertenece la segundo conjunto B, es decir  

4.3 Relaciones.

En matemática definimos relación como la correspondencia entre objetos o sujetos, y la representamos como un conjunto de pares ordenados. Por ejemplo:

4.4 Funciones.

Una función es una relación en la cual se tiene una correspondencia entre objetos; pero donde a cada elemento del conjunto de partida le corresponde una sola imagen en el conjunto de llegada. 

Diferencia entre Relación y Función.

Dominio y Rango

Algunos enlaces de interés:

Para que puedas aprender más sobre la unidad dejo aca unos enlaces muy interesantes:

http://www.luiszegarra.cl/moodle/mod/resource/view.php?id=24

Aplicaciones de Interés

http://mateludic.blogspot.com/2012/05/matematica-i-adm-guia-de-relaciones-y.html#comment-form

FACTORIZACIÓN

FACTORIZACIÓN

¿Qué es factorizar?

Es descomponer una expresión en dos o más factores, o dicho de otra forma, es expresar en multiplicandos una expresión cualquiera.

Por ejemplo:

Si tenemos la expresión 25 – 16. 

Podemos expresarla como: 5² –  4² = (5 – 4)(5 + 4)

Es lo que haremos con cualquiera de los términos que tengamos, pero con expresiones algebraicas.

Para FACTORIZAR, vamos a construir diferentes grupos de expresiones y las formas en las cuales se van a descomponer en factores.

Factor Común	Factor Común Monomio
	Factor Común por Agrupación de Términos
Binomios	Diferencia de Cuadrados
	Suma y Diferencia de Cubos
	Suma y Diferencia de n-ésima potencias
Trinomios	Trinomio Cuadrado Perfecto
	Trinomio de la forma x2 + bx + c
	Trinomio de la forma ax2 + bx + c

Veamos paso a paso como FACTORIZAR en cada caso:

FACTOR COMÚN MONOMIO

El factor común se determina así:

1)  El factor numérico el  M.C.D. de los coeficientes del polinomio.

2)  El factor literal está formado por aquellas letras que estén en todos los términos y elevados al menor exponente.

Ejemplo 1:27x3y2z - 18xyz2 + 9x2y3z = 9xyz (3x2y - 2z + xy2)

Ejemplo 2: 55x8/3 + 5x5/3 - 15x2/3 = 5x2/3 (11x6/3+x3/3-3) = 5x2/3 (11x2 + x- 3)

FACTOR COMÚN POR AGRUPACIÓN DE TÉRMINOS

Para  factorizar factor común por agrupación  de términos:

1. Se mira si el polinomio tiene un monomio común.

2. Si no tiene, se asocia  teniendo en cuenta los signos de tal manera que cada grupo tenga un  monomio común.

3. Se factoriza el polinomio común que genera la factorización de la agrupación anterior.

Ejemplos: factorizar

1. 4ay – 2by + 2az – bz = 2y(2a – b) + z(2a – b)

                        =  (2a – b) (2y + z)

2. 7ax + ay  – 7bx – by = (7ax +ay) – (7bx + by)   

                         =  a(7x + y) – b(7x + y)

                         =   (7x +y)(a – b)

EJERCICIOS:

Factorizar completamente cada polinomio por agrupación:

1.   6x – 6y – by + bx

2.   xm² + 2a + am² + 2x

3.   a – ab + b – b² + c – bc

4.   axy – bcz + bcxy – az

5.   a⁴ + a³ + a² + a

6.   –3a – 3b + 3(a + b)²

7.   8m³ – 2m² – 2mn + 8m²n

8.   12xy – 4y² – 6x + 2y

9.   (a + b) (a – b) + 4a – 4b

10.        x3b² – x²ya² + x³a² – x²b²y

FACTORIZACIÓN  DE DIFERENCIA DE CUADRADOS

Una diferencia de cuadrados  es igual a la suma de las raíces cuadradas de los términos, multiplicada por la diferencia de las misma.

x² – y² = (x + y) (x – y)

Ejemplo:  Factoricemos

49a²   –   9b² = (7a + 3b) (7a – 3b)

EJERCICIOS:

1.   a²  –   1_

            25

2.   16x² – 25y²

3.    a ² x² – b² y²

4.  x²  –    y²

   a²        b²             

5.    x^2a – y^2b

6.    a⁴b⁴ – 625c⁸    

7.    x⁴  –81

8.    (x  –a)² – (x + b)²

SUMAS Y DIFERENCIA DE CUBOS

1. Una suma o una resta de cubos es igual al producto de un binomio por un trinomio.

2. El binomio está formado por la suma o resta de raíces cúbicas.

3. El trinomio consta de: cuadrado de la primera raíz; producto de las dos raíces y cuadrado 

    de la segunda raíz.

4. Los signos del trinomio son:

a) Para suma de cubos: (+), (–), (+)

b) Para diferencia de cubos: (–), (+), (+)

x³ + y³ = (x + y)(x²  – xy + y²)

x³ – y³ = (x – y)(x²  + xy + y²)

Ejemplos:

1.  8x³  +  27y³  = (2x + 3y)[(2x)² – (2x)(3y) + (3y)²]  

EJERCICIOS:

1.   c³ – d³

2.   8a³ + 27b³

3.   a³ + 1

4.   (a – b)³ – 125

5.   8(m + n)³ – (3x)³

6   a³          b³

216        125

7.   a⁶ – b⁶

8.   a³ + b³ – a – b

9.   y⁹ + (m3 – 1)³

10. 64(m – n)³ – 8(m

TRINOMIO CUADRADO PERFECTO (TCP)

Un trinomio se llama cuadrado perfecto, si dos veces el producto de las raíces de los dos términos cuadrados perfectos, equivale al otro término.

Ejemplo:

a)  4x²  – 20xy  +  25y²  =  (2x – 5y)²   Es TCP

                           

b) 16a⁴ + 12a²b² +  9b⁴                No es TCP

     

EJERCICIOS:

*Completar el término que falta para que el trinomio sea cuadrado perfecto:

1.   x²  +2xy  + ____      

2.   a² + ____  +  25

3.   9x2  +18xy  +_____

4.   m²___  ___ + n²

5.   81a² – 18ab +___

6.   4x²___  ____ + 9

7.   ___ +4ab +b²

8.   9y² + 6xy + ___

9.  100a²___  ___ + 16

10  z² – 12zx – _____

*  Determinar cuáles de los siguientes polinomios son trinomios cuadrados perfectos:

1.    m² – 2m + 1

2.    t²   – 10t  + 25

3.    z² – 6z + 9

4.    x²  –  3x  + 6

5.    p²  –  pq  +  q²

6.    4b²  –  4b  +  1

7.    4x²  – 12x  +  9

8.    81u²  –  9uv  +  v²

TRINOMIO DE LA FORMA   x² + bx  +  c

Un trinomio es de la forma  x² + bx + c si existen números m y n  números reales  que cumplen  m.n = c y  b = (m + n), tales que   x² + bx + c = x² + (m + n)x + m.n.

Ejemplo:

a)            x² + 5x + 6 = x² + (3 + 2)x + 3.2

                             =  (x + 3)(x + 2)               

b)          x⁴ – 9x² – 22 = x⁴ + ((–11) + 2)x² + (–11).2

                             = (x² – 11)(x² + 2)

EJERCICIOS:

Factoriza:

1.   x2 – 2x – 15

2.   y2 – 13y + 22

3.   c² – 12c – 28

4.   b² + 19b + 84

5.   x² + 7x – 18

6.   a² – 2ab – 3b²

7.   z² + 15z + 26

8.   (m – n)² – 19(m – 2n) + 18

9.   x⁶ + 3x⁴ – 40x²

10.        a⁴ + 7a² – 18

TRINOMIO DE LA FORMA   ax²  +  bx  + c

Para factorizar trinomios de la forma  ax²  +  bx  + c, a ≠ 1, se expresa b como la suma de m y n enteros, tales que m.n = a.c y se agrupa para extraer el polinomio común así:

Ejemplo:

a) 3x² +  7x  +  2   =  3x²  +  6x  +  x  + 2 =  3x(x + 2) + (x + 2)

          

  

b) 6x² – 23x + 15 = 6x² – 18x – 5x + 15 =  6x(x – 3) – 5(x – 3)

                                 =  (x – 3)(6x – 5)

EJERCICIOS:

Factoriza:

1.   6x² – 13x  + 6

2.   12m² – 19m  – 18

3.   2x² – 3xy – 2y²

4.   15z² + 17zy –  4y²

5.   –7x² – 13y  + 2

6.   12x² – 22x  – 14

7.   32x + 108x² – 14x³

8.   33x² – 25xy + 2y²

9.   2x⁴ – x³ + 2x² – 9x + 4

10.        2x²(x – 1) – x² + 7x – 6